Giới thiệu về Markov Chain và ứng dụng

Markov Chain là một mô hình xác suất được sử dụng để mô tả các quá trình ngẫu nhiên dựa trên trạng thái trước đó Tuy mô hình này đơn giản nhưng nó lại được ứng dụng rộng rãi trong hầu hết các lĩnh vực trong đời sống nói chung và Machine Leaning nói riêng.

Bài viết này sẽ giới thiệu tổng quan về Markov Chain và các ứng dụng của nó, hướng dẫn chi tiết cách tính Markov Chain và triển khai bằng Python.

Khái niệm

Markov Chain (Chuỗi Markov) là một mô hình xác suất mô tả một chuỗi các sự kiện có thể xảy ra. Đặc điểm quan trọng của Markov Chain là tính memorylessness (không có trí nhớ), nghĩa là xác suất của một sự kiện tiếp theo chỉ phụ thuộc vào sự kiện hiện tại, các sự kiện trước đó sẽ không được ghi nhớ.

Hay nói cách khác, sự phân bố của các trạng thái tương lai chỉ phụ thuộc vào trạng thái hiện tại chứ không phụ thuộc vào cách nó đến trạng thái hiện tại, tính chất này còn được gọi là Markov Property hay Markovian (Tính Markov).

Một ván cờ có tính Markov, vì xác suất chiến thắng chỉ phụ thuộc vào vị trí hiện tại của các quân cờ, không phụ thuộc vào các nước đi trước đó. Trong khi đó, hành động lấy bóng trong một chiếc hộp có thể không có tính Markov, vì xác suất lấy được quả bóng cần tìm phụ thuộc vào các quả bóng đã lấy trước đó.

Các thành phần của Markov Chain

Giả sử có một dịch vụ thuê xe đạp gồm 3 trạm: $A$ , $B$ và $C$ .

Tất cả xe đạp phải được trả lại trạm vào cuối ngày tại một trạm nào đó trong 3 trạm trên. Sau khi kiểm tra tất cả các trạm vào mỗi cuối ngày. Ta nhận thấy rằng:

Trong các xe đạp mượn từ trạm $A$ , có $30\%$ được trả lại trạm $A$ , $50\%$ đến trạm $B$ và $20\%$ đến trạm $C$ .
Trong các xe đạp mượn từ trạm $B$ , có $10\%$ đến trạm $A$ , $60\%$ được trả lại trạm $B$ và $30\%$ đến trạm $C$ .
Trong các xe đạp mượn từ trạm $C$ , có $10\%$ đến trạm $A$ , $10\%$ đến trạm $B$ và $80\%$ được trả lại trạm $C$ .

Khi đó ta có thể biểu diễn Markov Chain của dịch vụ thuê xe đạp này như hình bên dưới.

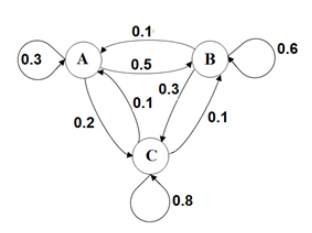
Mô phỏng ví dụ về Markov Chain — Source: math.libretexts.org

Qua đó, ta có thể thấy rằng Markov Chain có thể được biểu diễn bởi một Directed Networks (Mạng Có hướng), trong đó các đỉnh là tập hợp các State (Trạng thái) có thể xảy ra, với trọng số là xác suất chuyển từ một trạng thái này sang trạng thái khác.

📝 Nhắc lại
Trong Graph Theory, một Directed Networks (Mạng Có hướng) là sự kết hợp giữa Directed Graph (Đồ thị Có hướng) và Weighted Graph (Đồ thị Có trọng số).

State

State (Trạng thái) là một tập hợp các trạng thái có thể xảy ra trong Markov Chain.

Ở ví dụ trên, ta có 3 trạng thái là $\{A, B, C\}$ , vì một chiếc xe đạp khi muốn đưa về trạm thì chỉ xảy ra 1 trong 3 trường hợp này.

State Vector

State Vector (Vector Trạng thái) là một ma trận có một hàng mô tả xác suất của mỗi trạng thái trong Markov Chain.

\begin{align} \mathbf{Q} = \begin{bmatrix} q_1 & q_2 & \cdots & q_n \end{bmatrix} \end{align}

Ở ví dụ trên, giả sử tại thời điểm quan sát ban đầu, ta có $30%$ xe đạp ở trạm $A$ , $45%$ ở trạm $B$ và $25%$ ở trạm $C$ . Khi đó ta có vector trạng thái ban đầu là:

\begin{align*} \mathbf{Q}_0 = \begin{bmatrix} 0.3 & 0.45 & 0.25 \end{bmatrix} \end{align*}

Transition Matrix

Transition Matrix (Ma trận Chuyển tiếp) là một ma trận mô tả xác suất chuyển từ một trạng thái này sang một trạng thái khác trong Markov Chain.

\begin{align} \mathbf{P} = \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1n} \\ p_{21} & p_{22} & \cdots & p_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ p_{n1} & p_{n2} & \cdots & p_{nn} \end{bmatrix} \end{align}

Trong đó $p_{ij}$ là xác suất chuyển từ trạng thái $i$ sang trạng thái $j$ . Có thể kí hiệu là:

\begin{align} p_{ij} = P(X_{t+1} = \mathbf{Q}_j | X_n = \mathbf{Q}_i) \end{align}

Ở ví dụ trên, thay vì mô tả bằng graph (vừa không thân thiện với máy tính, vừa phức tạp khi có nhiều trạng thái), ta có thể mô tả bằng transition matrix sau:

\begin{align*} \mathbf{P} = \begin{bmatrix} 0.3 & 0.5 & 0.2 \\ 0.1 & 0.6 & 0.3 \\ 0.1 & 0.1 & 0.8 \end{bmatrix} \end{align*}

Lưu ý rằng transition matrix là một ma trận vuông, và các dòng của ma trận này phải có tổng bằng $1$ .

Các phép tính trên Markov Chain

Tìm xác xuất các trạng thái

Quay lại ví dụ vừa rồi, ta đã có transition matrix $P$ biểu diễn xác suất thay đổi trạm của các xe đạp, và vector trạng thái ban đầu $\mathbf{Q}_0$ biểu diễn xác suất phân bố giữa các trạm ban đầu.

Lúc này, ta có thể tính được xác suất phân bố của các chiếc xe đạp ở các trạm sau 1 ngày bằng cách tính $\mathbf{Q}_1$ như sau:

\begin{align*} \mathbf{Q}_1 &= \mathbf{Q}_0 \mathbf{P} \\ &= \begin{bmatrix} 0.3 & 0.45 & 0.25 \end{bmatrix} \begin{bmatrix} 0.3 & 0.5 & 0.2 \\ 0.1 & 0.6 & 0.3 \\ 0.1 & 0.1 & 0.8 \end{bmatrix} \\ &= \begin{bmatrix} 0.16 & 0.445 & 0.395 \end{bmatrix} \end{align*}

Vậy ta đã tính được sau ngày đầu tiên, xác suất các xe đạp ở các trạm $A$ , $B$ , $C$ lần lượt là $16\%$ , $44.5\%$ và $39.5\%$ .

Bây giờ, để tính được xác suất phân bố của các xe đạp ở các trạm sau 2 ngày, ta sẽ tính dựa trên state vector của ngày thứ nhất:

\begin{align*} \mathbf{Q}_2 &= \mathbf{Q}_1 \mathbf{P} \\ &= \begin{bmatrix} 0.16 & 0.445 & 0.395 \end{bmatrix} \begin{bmatrix} 0.3 & 0.5 & 0.2 \\ 0.1 & 0.6 & 0.3 \\ 0.1 & 0.1 & 0.8 \end{bmatrix} \\ &= \begin{bmatrix} 0.132 & 0.3865 & 0.4815 \end{bmatrix} \end{align*}

Vậy ta đã tính được sau ngày thứ hai, xác suất các xe đạp ở các trạm $A$ , $B$ , $C$ lần lượt là $13.2\%$ , $38.65\%$ và $48.15\%$ .

Tới đây, ta có thể rút ra được công thức tổng quát để tính xác suất phân bố của các xe đạp ở các trạm sau $n$ ngày:

\begin{align} \mathbf{Q}_n &= \mathbf{Q}_{n-1} \mathbf{P} \notag \\ &= \mathbf{Q}_0 \mathbf{P}^n \end{align}

Ta đã biết vì $\mathbf{Q}_1 = \mathbf{Q}_0 \mathbf{P}$ , nên $\mathbf{Q}_2 = \mathbf{Q}_0 \mathbf{P} \mathbf{P} = \mathbf{Q}_0 \mathbf{P}^2$ ,... Tuy nhiên ý nghĩa thực sự của $\mathbf{P}^n$ là gì?

Tìm xác suất chuyển trạng thái

Để giải quyết câu hỏi trên, ta sẽ thử tìm $\mathbf{P}^2$ :

\begin{align*} \mathbf{P}^2 &= \mathbf{P} \mathbf{P} \\ &= \begin{bmatrix} 0.3 & 0.5 & 0.2 \\ 0.1 & 0.6 & 0.3 \\ 0.1 & 0.1 & 0.8 \end{bmatrix} \begin{bmatrix} 0.3 & 0.5 & 0.2 \\ 0.1 & 0.6 & 0.3 \\ 0.1 & 0.1 & 0.8 \end{bmatrix} \\ &= \begin{bmatrix} 0.16 & 0.12 & 0.12 \\ 0.47 & 0.44 & 0.19 \\ 0.37 & 0.44 & 0.69 \end{bmatrix} \end{align*}

Từ định nghĩa của transition matrix tại $(2)$ , $\mathbf{P}$ còn cho ta biết biết xác suất chuyển trạng thái của xác xe đạp sau ngày đầu tiên.

Vậy, $\mathbf{P}^2$ chính là ma trận mô tả xác suất phân phối các trạng thái sau $2$ ngày. Ví dụ, xác suất một chiếc xe đạp chuyển từ trạm $A$ sang trạm $B$ sau $2$ ngày là $12\%$ .

Ta có công thức tổng quát để tính xác suất chuyển trạng thái sau $n$ ngày:

\begin{align} \mathbf{P}^n \end{align}

Ví dụ khác

Coca vs. Pepsi

Cho rằng:

Nếu loại nước ngọt gần nhất mà một người mua là $\text{Coca}$ , sẽ có $90\%$ khả năng người đó sẽ mua $\text{Coca}$ trong lần mua tiếp theo.
Nếu loại nước ngọt gần nhất mà một người mua là $\text{Pepsi}$ , sẽ có $80\%$ khả năng người đó sẽ mua $\text{Pepsi}$ trong lần mua tiếp theo.

Giả sử một người mua $\text{Coca}$ trong lần mua đầu tiên, hãy tính xác suất người đó sẽ mua $\text{Coca}$ trong lần mua thứ $3$ .

Ta lập transition matrix với $[\text{Coca}, \text{Pepsi}]$ là các trạng thái:

\begin{align*} \mathbf{P} &= \begin{bmatrix} 0.9 & 0.1 \\ 0.2 & 0.8 \end{bmatrix} \end{align*}

Với:

$P(\text{Coca} \rightarrow \text{Coca}) = 0.9$
$P(\text{Pepsi} \rightarrow \text{Pepsi}) = 0.8$
$P(\text{Pepsi} \rightarrow \text{Coca}) = 0.2$

Khi đó:

\begin{align*} & \ P(\text{Pepsi} \rightarrow \text{?} \rightarrow \text{Coca}) \\ =& \ P(\text{Pepsi} \rightarrow \text{Coca} \rightarrow \text{Coca}) + P(\text{Pepsi} \rightarrow \text{Pepsi} \rightarrow \text{Coca}) \\ =& \ 0.2 \times 0.9 + 0.8 \times 0.2 \\ =& \ 0.34 \end{align*}

Ta cũng có thể tính bằng cách tính $\mathbf{P}^2$ :

\begin{align*} & \ P(\text{Pepsi} \rightarrow \text{?} \rightarrow \text{Coca}) \\ =& \ \mathbf{P}^2_{\text{Pepsi}, \text{Coca}} \\ =& \begin{bmatrix} \_ & \_ \\ 0.2 & 0.8 \end{bmatrix} \begin{bmatrix} 0.9 & \_ \\ 0.2 & \_ \end{bmatrix} \\ =& \begin{bmatrix} \_ & \_ \\ 0.2 \times 0.9 + 0.8 \times 0.2 & \_ \end{bmatrix} \\ =& \begin{bmatrix} \_ & \_ \\ 0.34 & \_ \end{bmatrix} \\ =& \ 0.34 \end{align*}

Bài toán con chuột

Cho một con chuột sống trong căn nhà gồm $4$ phòng như sau:

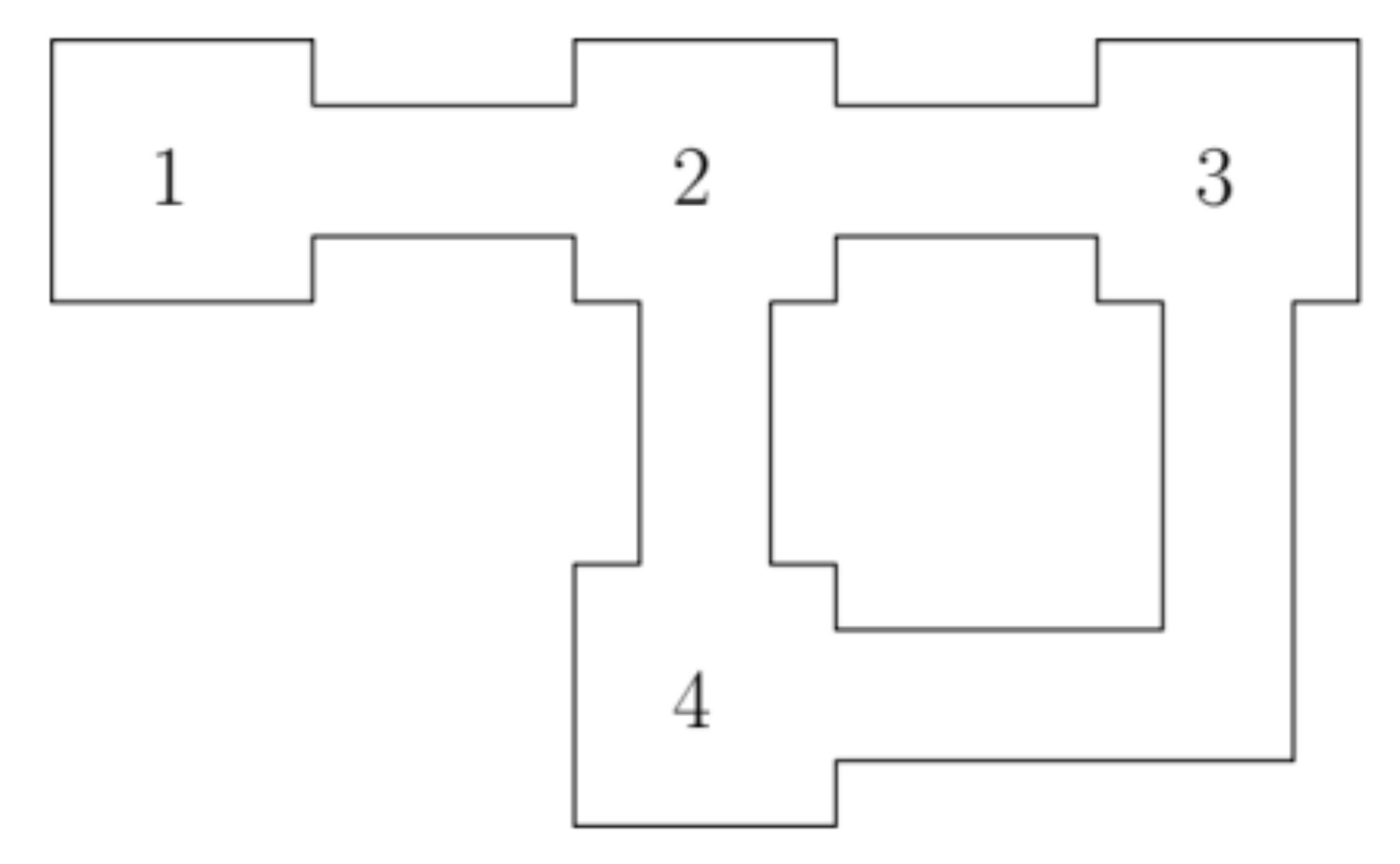
Mỗi ngày, con chuột sẽ lựa chọn ngẫu nhiên giữa việc ở lại phòng hiện tại với xác suất $1/4$ , hoặc di chuyển đến một phòng liền kề với xác suất $3/4$ .

Giả sử con chuột ban đầu ở phòng $1$ , hãy tính xác suất con chuột sẽ ở phòng $4$ sau $3$ ngày.

Ta lập transition matrix với $[1, 2, 3, 4]$ là các trạng thái:

\begin{align*} \mathbf{P} &= \begin{bmatrix} 1/4 & 3/4 & 0 & 0 \\ 1/4 & 1/4 & 1/4 & 1/4 \\ 0 & 3/8 & 1/4 & 3/8 \\ 0 & 3/8 & 3/8 & 1/4 \end{bmatrix} \end{align*}

Tính $\mathbf{P}^3$ :

\begin{align*} \mathbf{P}^3 &= \begin{bmatrix} 0.128 & 0.377 & 0.248 & 0.248 \\ 0.126 & 0.376 & 0.249 & 0.249 \\ 0.124 & 0.374 & 0.251 & 0.251 \\ 0.124 & 0.374 & 0.251 & 0.251 \end{bmatrix} \end{align*}

Do đó, xác suất con chuột từ phòng $1$ chuyển đến phòng $4$ sau $3$ ngày là $0.248$ .

Triển khai language model đơn giản bằng Markov Chain

Dựa vào ý tưởng của bài toán con chuột, ta có thể sử dụng Markov Chain để tạo ra văn bản ngẫu nhiên. Bằng cách nhập vào một từ bất kỳ, ta sẽ tạo ra một câu ngẫu nhiên với độ dài tuỳ ý.

Ví dụ khi ta nhập từ "I", sẽ có một xác suất sinh ra từ "can", và với từ "can", sẽ có một xác suất sinh ra từ "fix" hoặc "not", và với từ "not", sẽ có một xác suất sinh ra từ "fix",...

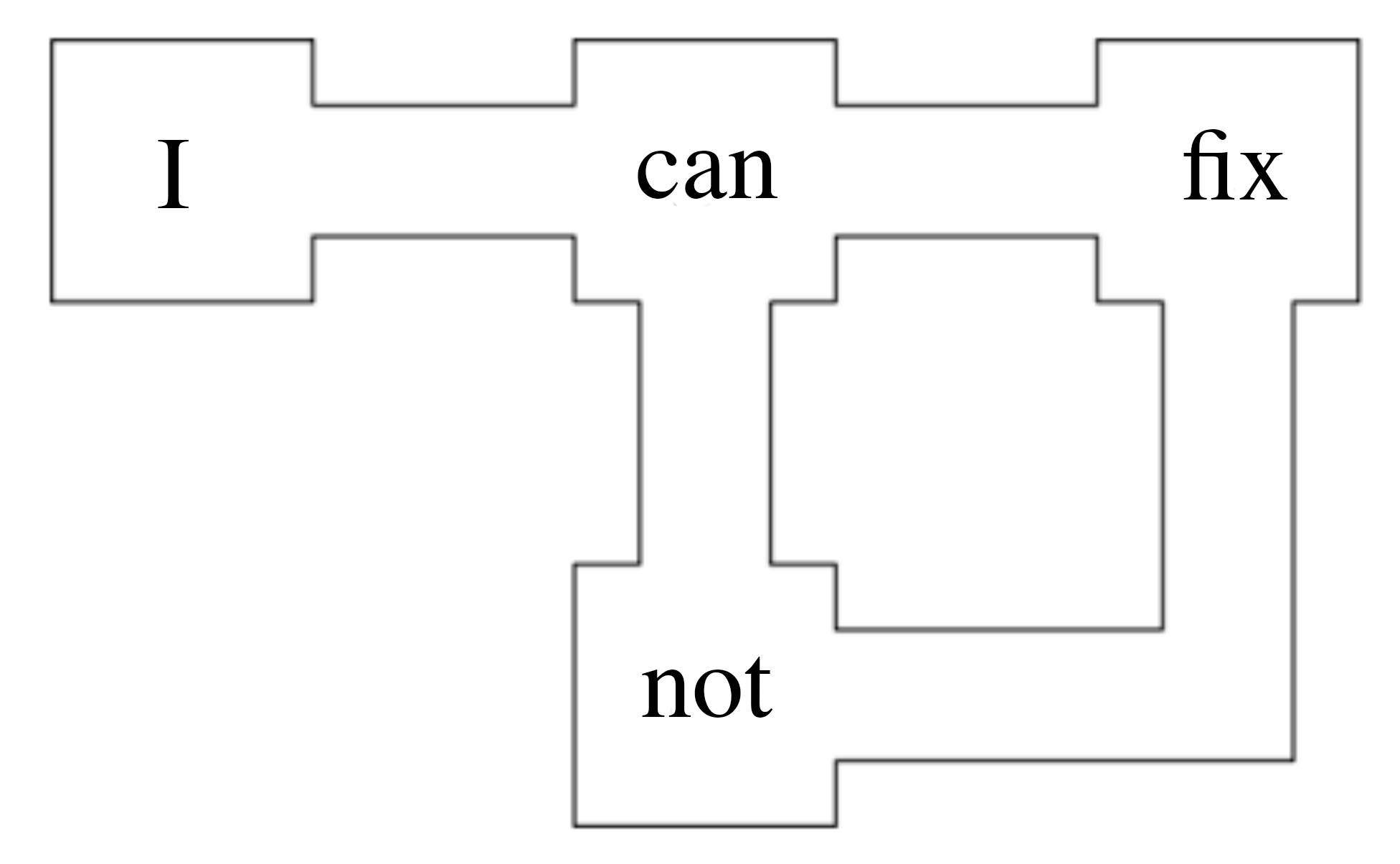
Mô phỏng ví dụ về language model đơn giản bằng Markov Chain

Để có thể triển khai được mô hình này, ta cần một đoạn văn lớn làm dữ liệu, và shakespeare.txt là một tập dữ liệu phù hợp cho ví dụ này.

Về lí thuyết, ta sẽ tách các bi-gram (cặp từ) trong đoạn văn đó ra làm các trạng thái, và tính xác suất chuyển trạng thái giữa các trạng thái đó.

Tuy nhiên để đơn giản hoá, ta sẽ sử dụng một dictionary với các key là các từ duy nhất trong đoạn văn, và các value là một list chứa các từ tiếp theo đã xuất hiện sau từ đó. Ví dụ:

{
    "I": ["can", "am", "do", "am", ...],
    "can": ["fix", "go", "not", "not", ...]
}

Toàn bộ code có thể xem chi tiết tại: snowyfield1906/ai-general-research/markov_chain /markov_chain.py.

Tiền xử lí và train model

class Markov():
    def __init__(self, file_path):
        self.file_path = file_path

        self.text = self.remove_punctuations(self.get_text())
        self.text = self.remove_newline(self.text)
        self.model = self.model()

    def get_text(self):
        text = []
        for line in open(self.file_path):
            text.append(line)
        return ' '.join(text)

    def remove_punctuations(self, text):
        return text.translate(str.maketrans('','', string.punctuation))

    def remove_newline(self, text):
        return text.replace('\n', '')

    def model(self):
        words = self.text.split(' ')

        markov_dict = defaultdict(list)

        for current_word, next_word in zip(words[0:-1], words[1:]):
            markov_dict[current_word].append(next_word)

        return dict(markov_dict)

Tạo câu ngẫu nhiên

def predict_words(chain, first_word, number_of_words=5):
    if first_word in list(chain.keys()):
        word1 = str(first_word)

        predictions = word1.capitalize()

        for i in range(number_of_words-1):
            word2 = random.choice(chain[word1])
            word1 = word2
            predictions += ' ' + word2

        predictions += '.'
        return predictions
    else:
        return "Word not in corpus"

Kiểm thử

m = Markov('./shakespeare.txt')
chain = m.model
output = predict_words(chain, first_word = 'but')
print(output)

> But that have bought me.

Ứng dụng

Markov Chain được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, xét riêng về Machine Learning, Markov Chain được sử dụng trong rất nhiều bài toán như:

Natural Language Processing (Xử lí Ngôn ngữ Tự nhiên)
Recommendation System (Hệ thống Gợi ý)
Reinforcement Learning (Học Tăng cường)
Computer Vision (Thị giác Máy tính)
Speech Recognition (Nhận dạng Giọng nói)
...

Trong đó, có 2 khái niệm quan trọng là Hidden Markov Model (Mô hình Markov Ẩn) và Markov Decision Process (Quy trình Quyết định Markov). Sẽ được giới thiệu trong các bài viết tiếp theo.