Phân tích chi tiết DEX dưới góc nhìn kĩ thuật (Phần 1

Trong hệ sinh thái DeFi, DEX đã nhanh chóng trở thành một phần quan trọng của việc trao đổi tài sản mã hoá và cung cấp thanh khoản. Điểm độc đáo của DEX so với các sàn truyền thống nằm ở việc chúng không cần sự can thiệp của bên thứ ba và hoạt động dựa trên các nguyên tắc của công nghệ Blockchain.

Trong bài viết này, chúng ta sẽ cùng nhau khám phá một cách chi tiết về cách hoạt động của DEX, tập trung vào hai mô hình phổ biến: Automated Market Maker (AMM) và Order Book. Bằng cách hiểu rõ cách mỗi mô hình hoạt động, chúng ta sẽ có cái nhìn sâu hơn về cách DEX đóng góp vào sự phát triển của hệ sinh thái DeFi.

Phân tích chi tiết DEX dưới góc nhìn kĩ thuật

Giới thiệu về DEX

Decentralized Exchange (DEX) là nền tảng cho phép người dùng trao đổi các tài sản mã hoá mà không cần đến sự trung gian của ngân hàng hay tổ chức truyền thống.

Một DEX bao gồm nhiều cặp tiền mã hóa để người dùng có thể trao đổi và mua bán trực tiếp các loại tiền mã hóa cho nhau. Hoạt động trên nguyên tắc của công nghệ Blockchain, DEX giúp tăng tính minh bạch, an toàn và ẩn danh trong giao dịch.

Hai mô hình phổ biến trong DEX là Automated Market Maker (AMM) và Order Book. Trong đó AMM là mô hình được sử dụng rộng rãi nhất, trong khi mô hình Order Book lại được sử dụng nhiều hơn trong các sàn giao dịch tập trung, gọi là Centralized Exchange (CEX).

Mô hình Automated Market Maker (AMM)

Các thuật ngữ cơ bản

Pool: Là cặp tiền mã hoá được sử dụng để trao đổi với nhau, thường kí hiệu là Base/Quote.
Base/Quote Token: Lần lượt là tiền mã hoá được dùng để Giao dịch và Định giá. Ví dụ trong cặp ETH/USDT, ETH là Base Token và USDT là Quote Token.
Swap: Lần lượt là hành động Mua và Bán một token trong một pool.
Liquidity: Là số lượng thanh khoản của một pool. Con số này biểu thị khả năng mua bán của một pool.
Liquidity Provider: Là người cung cấp thanh khoản cho một pool. LP sẽ nhận được phần thưởng từ phí swap.
Execution Price: Là giá trị thực tế mà một token được mua hoặc bán trong một giao dịch, đây là độ dài của đoạn thẳng nối 2 điểm giá (trước và sau) trên đồ thị.
Slippage: Là sự thay đổi giá của một token sau khi thực hiện swap. Slippage thường được tính bằng phần trăm.
Oracle: Là một dịch vụ cung cấp giá trị của một token, thông thường được sử dụng để định giá token trong một pool.

Khái niệm và nguyên tắc hoạt động của AMM

Automated market Maker (Tạo lập Thị trường Tự động) là một loại DEX rất phổ biến trong hệ sinh thái DeFi vì sự đơn giản và tối ưu của nó. AMM hoạt động dựa trên một công thức toán học để định giá một cặp tài sản, công thức này có thể khác nhau tùy vào từng giao thức, nhưng phổ biến nhất vẫn là Inverse Proportion Formula (Công thức Tỉ lệ Nghịch):

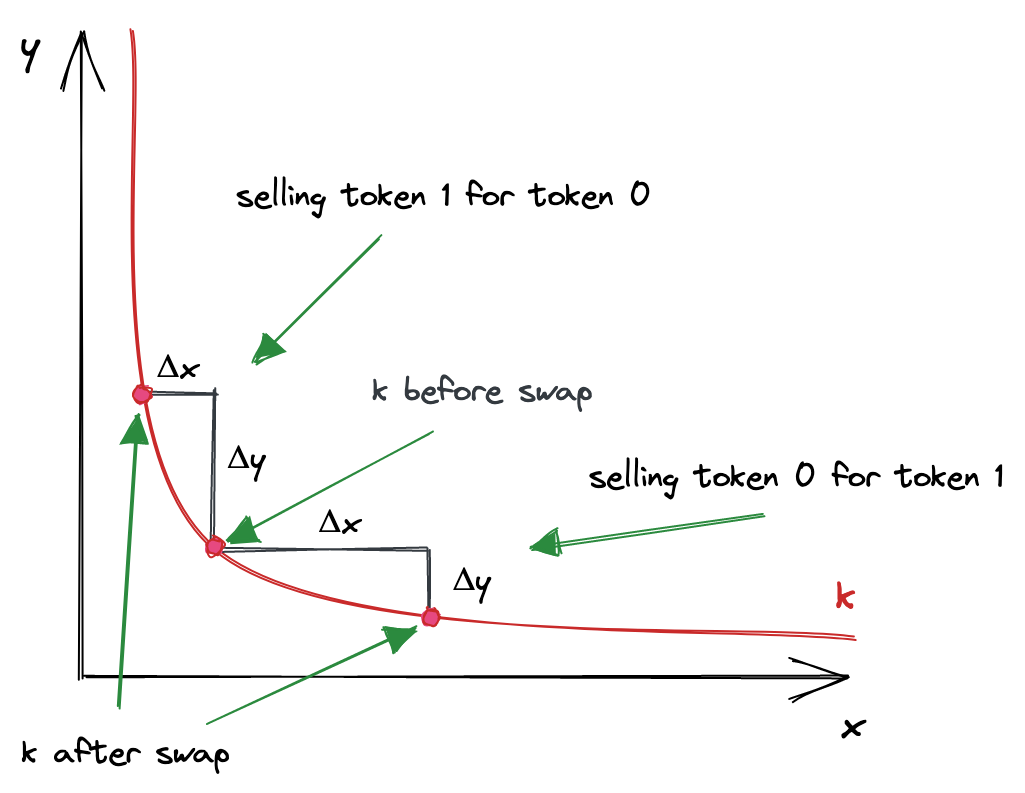
Công thức tỉ lệ nghịch — Source: uniswapv3book.com

Qua hình ảnh trên, ta thấy rằng khi số lượng của token này tăng lên thì số lượng của token kia sẽ giảm đi. Nó sẽ tự cân bằng bởi những người khác dựa trên quy luật cung cầu trong kinh tế.

Mỗi điểm trên đường cong biểu thị một trạng thái có thể xảy ra giữa số lượng của 2 token, lúc này giá của pool bằng với Hệ số của đường tiếp tuyến với đường cong tại điểm đó. Hệ số này còn được gọi là Đạo hàm của đường cong và nó đúng bằng với tỉ lệ giữa số lượng của 2 token. Nói cách khác, ‘Giá của token này là tỉ lệ giữa số lượng của token kia và chính nó’.

Điều quan trọng là, mấu chốt của AMM này là nằm ở LP, họ là những Market Maker (Nhà tạo lập thị trường) với nhiệm vụ cung cấp thanh khoản cho pool và nhận lại phần thưởng từ phí swap của người dùng.

Xác định giá trị của token

Công thức tỉ lệ nghịch

Đây là công thức được đề cập ở phía trên, dùng để cân bằng số lượng của hai token trong một pool:

xy = k \newline \implies \ x = \frac{k}{y} \quad \text{hay} \quad y = \frac{k}{x}

Trong đó:

$x$ là số lượng base token trong pool
$y$ là số lượng quote token trong pool
$k$ là một Constant Product (Tích hằng số) lớn hơn 0 và con số này không quan trọng

Vì $k$ là một hằng số nên khi $x$ tăng thì $y$ sẽ giảm và ngược lại. Số lượng của một loại tiền mã hóa và giá của nó trong pool sẽ không bao giờ bằng 0.

Mở rộng thêm, ta có công thức được sử dụng trong mọi giao dịch:

(x+ r\Delta x)(y-\Delta y) = k \newline

Trong đó:

$r = 1 + f$ là một hệ số với $f$ là phần trăm phí giao dịch, thường tính vào base token.
$\Delta x$ là số lượng base token muốn cho đi
$\Delta y$ là số lượng quote token muốn nhận lại

Khi mua một lượng token $y$ ( $\Delta y$ ), ta sẽ phải đặt vào pool một lượng token $x$ ( $\Delta x + f\Delta x$ ), gồm lượng token $x$ muốn đặt vào ( $\Delta x$ ) phí giao dịch ( $f\Delta x$ ). Phí giao dịch này sẽ được chia cho tất cả LP của pool đó.

Vì $k$ không bị thay đổi sau khi swap, chúng ta có thể tính được $\Delta y$ nhận được như sau:

\begin{align*} (x + r\Delta x)(y - \Delta y) &= xy \newline \iff y - \Delta y &= \frac{xy}{x + r\Delta x} \newline \iff -\Delta y &= \frac{xy}{x + r\Delta x} - y \newline \iff -\Delta y &= \frac{xy - y({x + r\Delta x})}{x + r\Delta x} \newline \iff -\Delta y &= \frac{xy - xy - y r \Delta x}{x + r\Delta x} \newline \iff -\Delta y &= \frac{- y r \Delta x}{x + r\Delta x} \newline \iff \Delta y &= \frac{y r \Delta x}{x + r\Delta x} \newline \end{align*}

Tương tự với $\Delta x$ :

\begin{align*} (x + r\Delta x)(y - \Delta y) &= xy \newline \iff x + r\Delta x &= \frac{xy}{y - \Delta y} \newline \iff r\Delta x &= \frac{xy}{y - \Delta y} - x \newline \iff r\Delta x &= \frac{xy - x(y - \Delta y)}{y - \Delta y} \newline \iff r\Delta x &= \frac{xy - xy + x \Delta y}{y - \Delta y} \newline \iff r\Delta x &= \frac{x \Delta y}{y - \Delta y} \newline \iff \Delta x &= \frac{x \Delta y}{r(y - \Delta y)} \newline \end{align*}

Công thức tính giá của token

Ta có thể chứng minh Đạo hàm của đường cong tại một điểm bất kì bằng với tỉ lệ giữa số lượng của hai token:

\begin{align*} y &= \frac{k}{x} \newline \iff \frac{dy}{dx} &= \frac{d}{dx}(\frac{k}{x}) \newline \iff \frac{dy}{dx} &= -\frac{k}{x^2} \newline \iff \frac{dy}{dx} &= -\frac{y}{x} \newline \end{align*}

📝 Nhắc lại
Đường thẳng tiếp tuyến với đường cong tại điểm giá $(x_0, y_0)$ có phương trình:
$\begin{align*} y &= \left. \frac{dy}{dx} \right|_{(x_0, y_0)}(x - x_0) + y_0 \newline y &= -\frac{y_0}{x_0}(x - x_0) + y_0 \newline y &= -\frac{y_0}{x_0}x + 2y_0 \newline \end{align*}$

Tóm lại, dựa theo hệ số của đường tiếp tuyến, ta có công thức tính giá của token như sau:

P_{x} = \frac{y}{x} \quad \text{và} \quad P_{y} = \frac{x}{y} \newline

Trong đó:

$P_{x}$ là giá của token $x$ đối với token $y$
$P_{y}$ là giá của token $y$ đối với token $x$

Ví dụ minh họa

Giả sử ta có một pool với 2 token là $x$ và $y$ có số lượng ban đầu đều là $100$ , khi đó giá của pool lúc này sẽ là:

P = P_{x} = \frac{y}{x} = \frac{100}{100} = 1

Cho rằng pool có phí là $f = 1\%$ ( $r = 1.01$ ), khi ta thực hiện bán $10$ token $x$ , ta sẽ phải trả thêm $f\Delta x = 0.1$ token $x$ vào pool. Và $\Delta y$ nhận được sẽ là:

\begin{align*} \Delta y &= \frac{y r \Delta x}{x + r\Delta x} \\ &= \frac{100 \times 1.01 \times 10}{100 + 1.01 \times 10} \\ &= 9.173478655767484\ldots \end{align*}

Chúng ta cũng tính được giá của pool sau khi swap:

\begin{align*} P &= P_{x} \\ &= \frac{y - \Delta y}{x + r\Delta x} \\ &= \frac{100 - 9.173478655767484}{100 + 10.1} \\ &= 0.82494569794943252\ldots \end{align*}

Ta cũng có thể kiểm tra lại hệ số $k$ :

\begin{align*} k &= x y \\ &= 110.1\times 90.82652134423252\ldots \\ &= 10000 \\ &= 100 \times 100 \end{align*}

Các phép tính liên quan đến LP

LP token

Bởi vì giá chỉ thay đổi khi swap được thực hiện, nên khi các LP cung cấp liquidity cho pool, họ phải cung cấp cả hai token với tỉ lệ đúng bằng tỉ lệ của giá hiện tại để tránh làm thay đổi nó.

Để dễ hình dung, đường cong của pool chính là một chiếc cân Roberval với hai đĩa, mỗi đĩa đại diện cho một token và giá của pool chính là mũi tên cân bằng. Khi bỏ vào một lượng token, mũi tên sẽ nghiêng đi một đoạn, hay nói cách khác là giá của nó sẽ dịch chuyển một đoạn. Để giữ cho mũi tên cân bằng tránh bị dịch chuyển, ta phải cung cấp thêm token còn lại.

Các LP sẽ nhận được LP token của DEX hoặc pool đó với số lượng là lượng liquidity mà họ đã cung cấp, lượng này liquitiy sẽ được tính tùy theo từng pool.

Các LP cũng có thể trade token này hoặc đốt (rút khỏi pool) một lượng bất kì để nhận lại cặp token tương xứng mà họ đã bỏ vào pool, đồng thời họ cũng sẽ nhận được ít lợi tức hơn khi người dùng swap.

Giá trị của một LP token được tính theo công thức sau:

P_\text{LP} = \frac{P_\text{T}}{C}

Trong đó:

$P_\text{LP}$ là giá trị của một LP token
$P_\text{T}$ là tổng giá trị của tất cả token trong pool
$\text{C}$ là tổng số lượng LP token đang lưu hành

Ví dụ cặp ETH/USDT với ETH có giá là $2000$ $ và USDT có giá là $1$ $. Cho rằng trong pool có $2$ ETH và $4000$ USDT, khi đó giá của pool sẽ là:

\begin{align*} P_\text{T}\space (\$) &= P_{ETH} + P_{USDT} \\ &= 2 \times 2000 + 1 \times 4000 \\ &= 8000 \$ \end{align*}

Nếu đang có $1000$ LP token đang lưu hành, khi đó giá của một LP token sẽ là:

P_\text{ETH/USDT token} = \frac{8000}{1000} = 8 \$

Lợi tức của LP

Khi có một lượng LP token, các LP sẽ nhận được hoa hồng miễn là đang có swap xảy ra. Khi đó:

\text{E} \space (liquidity)= \frac{L}{L_T} \times \Delta L_f \space (liquidity)

Trong đó:

$\text{E}$ là lợi tức nhận được tính theo liquidity
$L$ Lượng liquidity đang cung cấp
$L_T$ Lượng liquidity của pool
$\Delta L_f$ Lượng phí mà người swap trả tính theo liquidity (tương đương $f\Delta x$ )

Ví dụ cặp ETH/USDT ( $0.3\%$ ) có liquidity là $8000$ và ta có $1000$ LP token, khi đó với một lượt swap có phí bằng 100 liquidty, ta sẽ nhận được:

\begin{align*} \text{E} \space (liquidity) &= \frac{1000}{8000} \times 100 \\ &= 12.5 \space (liquidity) \end{align*}

Trượt giá

Giới thiệu

Trong mô hình này, việc trượt giá thường xuyên xảy ra, đây là hiện tượng giá thực tế mà người dùng nhận được sau khi thực hiện một giao dịch không giống như giá được hiển thị ban đầu trên giao diện. Thường xảy ra ở những pool có lượng liquidity thấp và khối lượng giao dịch cao.

Cụ thể, khi một giao dịch được xử lí trong lúc có một lượng lớn các giao dịch khác được thực hiện, các giá trị được tính toán trong giao dịch này sẽ khác (xa) so với các giá trị hiển thị trên giao diện, khi đó chúng ta sẽ không nhận được số token như mong đợi.

Do đó, hầu hết các DEX đều có một cơ chế trượt giá, chúng ta sẽ nhập vào một khoảng trượt giá có thể chấp nhận được, nếu giá thực tế vượt quá giá cho phép, giao dịch sẽ bị hủy.

Cách tính

Quay lại Ví dụ minh họa, nếu không xảy ra trượt giá, ta sẽ nhận được toàn bộ $9.173478655767484\ldots$ token $y$ với $10.1$ token $x$ , do đó mức giá $0.82494569794943252\ldots$ tính được chính là Giá tuyệt đối.

Tuy nhiên, giả sử xảy ra trượt giá khi mà chúng ta chỉ nhận được $9.0$ token $y$ với $10.1$ token $x$ , khi đó ta tính được Giá thực tế là $0.8910891089108911\ldots$

Lúc này, đã xảy ra trượt giá với độ trượt giá được tính như sau:

\begin{align*} \text{S} \space (\%) &= \frac{| P_P - P_A |}{P_A} \times 100\% \\ &= \frac{| 0.82\ldots - 0.89\ldots |}{0.82\ldots} \times 100\% \\ &= 0.08\ldots \times 100\% \\ &= 8.01\ldots \ldots \% \end{align*}

Trong đó:

$\text{S}$ là độ trượt giá
$P_P$ là giá tuyệt đối
$P_A$ là giá thực tế

Như vậy đã xảy ra trượt giá $\approx 8\%$ . Giả sử nếu chúng ta cài đặt độ trượt giá là $5\%$ , giao dịch này sẽ bị hủy.

Ưu nhược điểm của AMM

Ưu điểm

Đơn giản: AMM là một mô hình đơn giản, dễ hiểu và dễ sử dụng. Phù hợp cho những người chỉ cần swap token một cách nhanh chóng mà không cần quan tâm đến những thứ khác.
Không yêu cầu liquidity cao: AMM vẫn có thể hoạt động tốt trong một thị trường có liquidity thấp, điều này rất thích hợp cho các DEX.

Nhược điểm

Trượt giá: Trượt giá có thể thường xuyên xảy ra trên các AMM DEX. Một lệnh swap lớn, một pool đang có khối lượng giao dịch cao hoặc liquidity thấp đều dẫn đến trượt giá.
Dễ bị tấn công: Vì AMM là một mô hình đơn giản, nên nó khá dễ bị tấn công bởi nhiều cách.

Vậy là chúng ta đã đi qua cách hoạt động của mô hình AMM. Đến với Phần 2 - Order Book, chúng ta đã tìm hiểu về cách hoạt động của một Order Book.